Czym jest dyskalkulia?
Dyskalkulia jest deficytem dotyczącym nabywania podstawowych zdolności numerycznych (bazowych kompetencji przetwarzania liczb) występującym przy jednoczesnej normie intelektualnej (ilorazie inteligencji w normie). Oznacza to, że problem osoby z dyskalkulią dotyczy wybiórczo umiejętności związanych z matematyką, podczas gdy nie wykazuje ona innych deficytów. Należy jednak pamiętać, że „czysta” dyskalkulia występuje bardzo rzadko, zaś znacznie częściej spotykamy się ze współwystępowaniem tego zaburzenia z innymi, np. dysleksją czy deficytami uwagi. Literatura podaje, że osoby cierpiące na dyskalkulię stanowią 3-6% ogólnej populacji. Trzeba jednak wiedzieć, że wiele osób z dyskalkulią nie jest diagnozowanych, jak również nierzadko stawiana jest niewłaściwa diagnoza (diagnozuje się dyskalkulię, podczas gdy problem leży zupełnie gdzie indziej, np. w deficytach funkcji językowych czy pamięciowych). Często przyczyną są niedoskonałe narzędzia diagnozy.
Literatura wskazuje, że konsekwencje wynikające z dyskalkulii, zarówno te dotykające jednostkę, jak i społeczeństwo, są znacznie bardziej dotkliwe niż te wynikające np. z dysleksji. Osoby z dyskalkulią mniej zarabiają, częściej chorują, wymagają więcej wsparcia w szkole, a nawet częściej popadają w konflikt z prawem. Co więcej, analizy prowadzone przez takie organizacje jak OECD wskazują, że trudności w zakresie matematyki wprost rzutują na sytuację ekonomiczną kraju.
Najnowsza klasyfikacja DSM-V (Diagnostic and Statistical Manual of Mental Disorders), definiuje szeroko “specyficzne zaburzenie uczenia się”, jednak występujące w trzech podtypach: 1. trudności w czytaniu; 2. w pisemnym wypowiadaniu się; 3. w matematyce, w miejsce trzech odrębnych zaburzeń (definiowanych uprzednio). Co ważne, klasyfikacja DSM-V odmiennie (w porównaniu z poprzednią) odnosi się do zależności między wspomnianymi specyficznymi trudnościami w uczeniu się a inteligencją mierzoną jako IQ. W DSM-IV jednym z koniecznych warunków diagnozy specyficznych zaburzeń w uczeniu się była rozbieżność między wynikami testów osiągnięć szkolnych a poziomem inteligencji (która powinna pozostawać w normie przy relatywnie niskich osiągnięciach). Natomiast w DSM-V odchodzi się od tego kryterium. Jeśli więc stwierdza się trudności w opanowaniu umiejętności szkolnych, trudne do wyjaśnienia zaniedbaniem, błędami w edukacji, niepełnosprawnością intelektualną, innymi zaburzeniami neurologicznymi lub umysłowymi, wówczas stawiamy diagnozę specyficznego zaburzenie uczenia się, niezależnie od rozbieżności między IQ i testach kompetencji szkolnych w zakresie czytania, pisania i matematyki. Dyskutowaną przez badaczy i praktyków kwestią jest to, czy iloraz inteligencji wykazuje związek z nauką czytania, pisania i arytmetyki, a ściślej z tymi ich aspektami, które stanowią objawy wspomnianych specyficznych zaburzeń w uczeniu się i, czy jeśli inteligencja nie koreluje z nabywaniem tych umiejętności, to czy należy traktować IQ jako jedno z kryteriów diagnozy (tu: m.in. dyskalkulii). Można też zadać pytanie o to, które obszary inteligencji (np. wyniki których podskal w Skali Inteligencji Wechslera) mogą być związane z zaburzeniami uczenia się matematyki, a które nie.
Wedle klasyfikacji ICD-10 natomiast dyskalkulia to specyficzne zaburzenia umiejętności arytmetycznych, które nie może być wyjaśniane niewłaściwymi metodami edukacji matematycznej ani obniżonymi możliwościami intelektualnymi dziecka (opóźnionym rozwojem umysłowym), a specyficzne trudności w uczeniu się matematyki można rozpoznać na podstawie wyniku testu do badania umiejętności arytmetycznych istotnie niższego od oczekiwanego na podstawie wieku i IQ. Ponadto, wyniki testów czytania i pisania powinny jednocześnie pozostawać w normie oraz wiadomo, że trudności w operowaniu liczbami nie są efektem wad wzroku ani słuchu.
Typowe problemy osób z dyskalkulią
Dyskalkulia jest wynikiem zaburzonego tzw. zmysłu numerycznego (ang. number sense), wrodzonej bazy podstawowych kompetencji numerycznych, którego najbardziej wyraźnym przejawem, widocznym już u bardzo małych dzieci, jest m.in. zdolność do szacowania liczebności zbiorów oraz umiejętność szybkiego dokładnego określania liczby niewielu obiektów (do 4 elementów włącznie), nazywana subitacją. Ma on swoje neuronalne podstawy w korze ciemieniowej. Dzieci z dyskalkulią, w porównaniu z prawidłowo rozwijającymi się rówieśnikami, wykazują problemy w zakresie tak elementarnych umiejętności jak przeliczanie obiektów, nazywanie czy porównywanie liczb, zadania arytmetyczne (obliczenia dokładne i przybliżone), wydobywanie faktów arytmetycznych (takich jak np. „5 + 13 = 18”). Dzieci te stosują też często niedojrzałe i nieskuteczne strategie w takich zadaniach (np. bardzo długo utrzymuje się przeliczanie na palcach) oraz błędnie szacują liczebności, odległości, wysokości i czas. Osoby z dyskalkulią ujawniają także niski poziom szacowania miejsca liczb na osi, a więc nie operują prawidłowo tzw. mentalną osią liczbową (Mental Number Line, MNL).
Dyskalkulii nie da się całkowicie wyleczyć ani też nigdy się z niej nie „wyrasta”. Można (i na pewno warto podjąć wysiłek w tym kierunku) próbować pokonywać deficyty typowe dla dyskalkulii, aby złagodzić problemy obecne w tym przypadku, po to by móc radzić sobie w codziennym funkcjonowaniu z tym deficytem.
Podłoże neuronalne
Co wiadomo z badań nad organizacją mózgu u osób z trudnościami w przetwarzaniu materiału numerycznego? Wykazano, że zaburzone operowanie reprezentacjami liczb idzie w parze z nieprawidłowościami w obrębie obszarów będących podstawą neuronalną MNL. Wszystko to dodatkowo potwierdza, że liczby są reprezentowane w umyśle m.in. przestrzennie oraz, że ta relacja numeryczno-przestrzenna ma istotny wpływ na poziom umiejętności matematycznych, zaś formowanie się MNL jest jednym z kluczowych kroków w rozwoju tych umiejętności. Neuroobrazowanie mózgu osób z dyskalkulią ujawniło m.in. atypową głębokość tzw. bruzdy śródciemieniowej oraz redukcję poziomu aktywacji w obrębie sieci czołowo-ciemieniowej podczas porównywania liczb (w formacie zarówno niesymbolicznym i symbolicznym) oraz podczas wykonywania zadań arytmetycznych. Ponadto, u osób z dyskalkulią obserwuje się mniejszą objętość substancji szarej w lewej bruździe śródciemieniowej, choć niektórzy badacze stwierdzili tego rodzaju redukcję objętości w tym obszarze w obu półkulach. Badania nad funkcjonalnymi połączeniami pomiędzy obszarami ciemieniowymi zaangażowanymi w przetwarzanie liczb oraz połączeniami między korą ciemieniową i potyliczno-skroniową wykazały też, że u osób z dyskalkulią wzorzec współaktywowania się tych struktur nie jest prawidłowy.
Zależności numeryczno-przestrzenne
Wyniki badań klinicznych oraz behawioralnych i psychofizjologicznych z udziałem zdrowych ochotników potwierdzają istnienie wyraźnej relacji między liczbami i przestrzenią (ang. Spatial-Numerical Association, SNA), gdyż przetwarzanie liczb i przestrzeni ma wspólne neuronalne podłoże. Układ przestrzenny liczb znajduje swoje odzwierciedlenie w wykonaniu zadań opartych na tej relacji (np. wpływa na czas odpowiedzi na liczby o określonej wielkości numerycznej). Zależność liczbowo-przestrzenna została dowiedziona u dzieci w okresie wczesnoszkolnym, przedszkolnym, a nawet u niemowląt i u różnych gatunków zwierząt.
Opisano szereg przejawów jej istnienia, co oznacza, że oba typy informacji wchodzą w interakcję na wiele sposobów. Jednak nie wszystkie korelują z poziomem umiejętności matematycznych lub korelacja ta wydaje się być co najmniej dyskusyjna. Jednym z efektów ilustrujących zależność między liczbami i przestrzenią jest tzw. efekt SNARC (ang. Spatial Numerical Association of Response Codes), który jest obszernie udokumentowany w literaturze i stanowi wyraźny marker tej relacji. Manifestuje się on tym, że na liczby o wyższej wartości liczbowej reagujemy szybciej, gdy odpowiedź udzielana jest po prawej stronie ciała (np. prawą ręką lub stopą, ruchem oczu w prawo), natomiast na liczby o niskiej wartości – gdy odpowiedź jest udzielana za pomocą reakcji po lewej stronie.
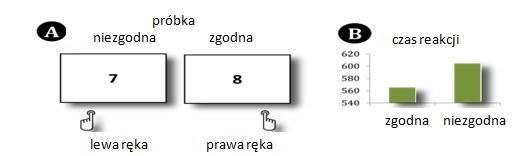
Efekt ten udało się zreplikować w licznych badaniach przy użyciu bardzo różnych zadań eksperymentalnych oraz rodzajów bodźców (wzrokowych, słuchowych, w różnym formacie: zbiory kropek, cyfry, liczebniki) i widoczny jest nawet wtedy gdy sama wartość liczbowa jest nieistotna dla zadania. Co wpływa na siłę tego efektu? Badania dowodzą, że np. takie czynniki kulturowe, jak kierunek pisania i czytania modulują kierunek tej zależności (niskie liczby-lewo, wysokie-prawo) odwracając go lub przekładając się na jego mniejszą siłę czy całkowity jego brak. To tylko dodatkowo dowodzi, że relacja numeryczno-przestrzenna jest uwarunkowana biologicznie, zaś wpływy środowiskowe (doświadczenie) wyraźnie „nakładają” się w swoim oddziaływaniu na biologiczne podstawy.
Co ciekawe jednak, siła tego efektu niekoniecznie koreluje z poziomem umiejętności arytmetycznych dzieci lub zależność ta jest co najmniej dyskusyjna. Wyniki niektórych badań wskazują na istnienie pozytywnego związku między siłą efektu SNARC i poziomem kompetencji numerycznych, a więc sugerują, że im bardziej wyraźna jest wspomniana zależność liczbowo-przestrzenna tym wyższy poziom umiejętności matematycznych. Jednak inne badania ujawniły wręcz przeciwną zależność: niski poziom umiejętności matematycznych idzie w parze z dużą siłą efektu SNARC, jak również są dane wskazujące na brak takiej korelacji w ogóle. Należy jednak dodać, że związek między siłą efektu SNARC i poziomem kompetencji matematycznych zdaje się zależeć dodatkowo od wieku. Badania z dorosłymi wskazują, że im wyższy poziom umiejętności tym słabszy efekt, podczas gdy badania z dziećmi sugerują, że lepsze kompetencje idą w parze z silniejszym efektem SNARC.
Część danych z literatury naukowej sugeruje, że zadanie, w przypadku którego poziom wykonania jest wyraźnym predyktorem kompetencji arytmetycznych jest szacowanie miejsca liczby na osi liczbowej (ang. Number Line Estimation). Wymaga ono operowania MNL, więc również odnosi się do ukierunkowanego (lewo-prawo) uporządkowania przestrzennego umysłowych reprezentacji liczb. Polega ono na pomiarze zdolności do przestrzennej lokalizacji liczby na osi pozbawionej zarówno podziałki jak i zaznaczonych na niej wartości (z wyjątkiem początkowej i końcowej).

Precyzja takiego szacowania miejsca liczb na osi zmienia się w prawidłowym rozwoju dziecka idąc w kierunku coraz lepszego dopasowywania miejsca poszczególnych liczb do ich lokalizacji na osi. U dzieci z dyskalkulią natomiast obserwuje się wysokie wartości błędu takiego szacowania i poziom wykonania takiego zadania typowy dla dzieci młodszych. Dlatego zdaniem niektórych badaczy, wysoka precyzja w lokalizowaniu miejsca liczb na osi jest predyktorem umiejętności szkolnych w zakresie arytmetyki.

